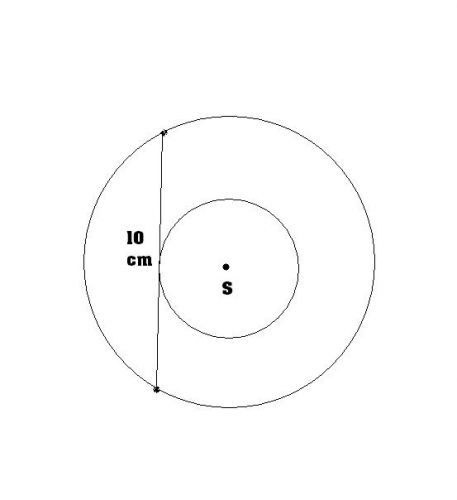
Jak zjistíme obsah mezikruží, jestliže známe pouze úsečku o délce 10 cm, která se dvěma body dotýká vnější kružnice a jedním bodem vnitřní? (bez použití vzorce na výpočet obsahu mezikruží, pokud to jde, děkuji za nápovědy)
0x
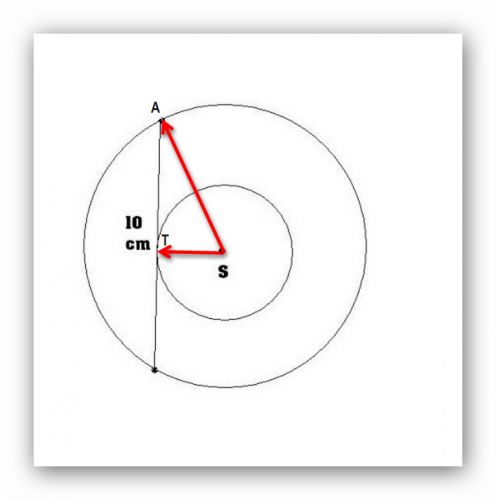
Dopsaljsem vám do obrázku dva body a dva poloměry . |AS| budiž R (ploměr větší kružnice), |TS| budiž r (poloměr menší kružnice). No a dál... použijte na trojúhelník ATS Pythagorovu větu a obsah mezikruží spočtěte jako rozdíl obsahů většího a menšho kruhu.
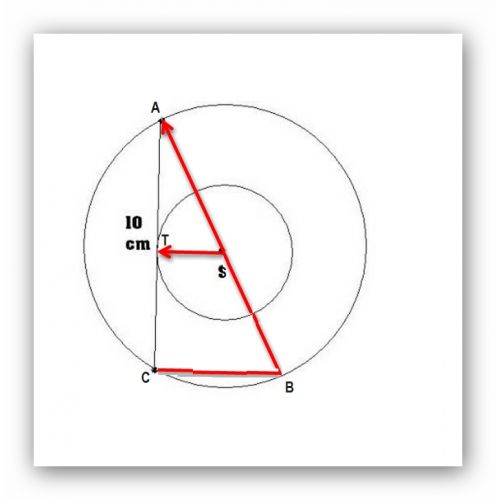
Vy jste ovšem chtěl výpočet bez použití vzorečku pro obsah mezikruží, a to tady asi není. Ono se sice zdá, že to nejde, počítáte obsah a nějaký vzorec pro obsah potřebujete, ale stejně vám dám radu. Nejprve zdvojnásobte trojúhelník AST tak, abyste dostal trojúhelník ABC a pak použijte Pythagora na něj. Ale trochu si ji upravte. Jestliže obsah čtverce o sraně a je a2, tak obsah kruhu o průměru a je ¼πa2, tedy násobek obsahu čtverce. To umožní přeformulovat Pythagora takto:
U pravoúhlého trojúhelníka o odvěsnaách a, b a přeponě c je součet obsahů kruhů o poloměrech a,b roven obsahu kruhu o poloměru c.
doplnené 11.05.14 08:22:Oprava: chtěl jsem upravenou P.v. napsat v podobě
U pravoúhlého trojúhelníka o odvěsnaách a, b a přeponě c je součet obsahů kruhů o průměrech a,b roven obsahu kruhu o průměru c.
Tak, jak jsem to napsal původně, to sice platí taky (i když bych to odvozoväl nepatrně jinak), ale pro naše účely se lépe hodí uvedená formulace.
0x
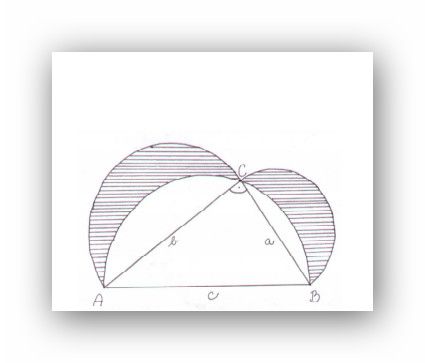
Řešit tuto úlohu, jak jsem ostatně již napsal, bez znalosti vzorce pro obsah mezikruží je možné, ale nakonec budu muset znát aspň vzorec pro obsah kružnice. Myšlenka je podobná jako při řešení úlohy na Hippokratovy měsíčky, viz přiložený obrázek, kdy máte spočítat obsah vyšrafovaných srpků. Řešení zde vycházá z toho, že obsah polokruhu o poloměru a ja pevným násobkem obsahu čtverce o straně a. Přímočarý důkaz vychází z toho, že obsah polokruhu o průměru a je roven 1/8(πa²![]() , zatímco obsah čtverce o straně a je a², ale není to jediný možný přístup. Stačí si uvědomit, že všechny čtverce i všechny polokruhy jsou si podobné. takže spošítáte-li (jakkoli) ten poměr pro a = 1, z podobnosti je jasné, že změnou a se tento poěr nezmění. Takže vyvásobíte.li vztah z Pythagorovy věty
, zatímco obsah čtverce o straně a je a², ale není to jediný možný přístup. Stačí si uvědomit, že všechny čtverce i všechny polokruhy jsou si podobné. takže spošítáte-li (jakkoli) ten poměr pro a = 1, z podobnosti je jasné, že změnou a se tento poěr nezmění. Takže vyvásobíte.li vztah z Pythagorovy věty
c2 + b2 = c2
tímto poměrem, tak můžete vyslovit P, větu v podobě
Součet obsahů polokruhů nad odvěsnami je rpven obsahu polokruhu nad přeponou
a z této formulace snadno zjistíte, že obsah Hippokratových menisků je roven obsahu trojúhelníka ABC z obrázku. Takže zde nakonec ani vzorec pro obsah půlkruhu nepotřebujete.
Podobně u vaší úlohy snadno zjistíte, ře obsah mezikruží je roven obsahu kruhu o průměru 10cm (respektive o poloměru 5cm), aniž byste potřeboval znát vzorec nejen pro obsakh mezikruží, ale ani vzorec pro obsah kruhu. (postup jsem již naznačil, stačí použít Pyt.větu například v podobě: U pravoúhlého trojúhelníka o odvěsnaách a, b a přeponě c je součet obsahů kruhů o poloměrech a,b roven obsahu kruhu o poloměru c.) Pokud tato odpověď stačí, tak takový vzorec nepotřebujete vůbec, poku chcete obsah vyčíslit, tak budete muset použít aspoň ten vzorec pro kruh.
Pomohlo vám to? Prosím, napište.
Nenesieme zodpovednosť za správnosť informácií a za škodu vzniknutú ich využitím. Jednotlivé odpovede vyjadrujú názory ich autorov a nemusia sa zhodovať s názorom prevádzkovateľa poradne Poradte.sk
Používaním poradne súhlasíte s personalizovanou reklamou, ktorá pomáha financovať tento server, ďakujeme.