Dobrý deň,
chcel by som poprosiť o pomoc s matematickou úlohou.
V rovine máme N bodov. Máme nájsť najmenší možný polomer takého kruhu, na ktorom leží M z nich,
pričom:
M<=N.
Máme daných N súradníc bodov v rovine.
Príklad:
Máme 3 body (N) a 3 z nich (M) musí ležať v kruhu s čo najmenším polomerom. Ich súradnice sú[-1,-1], [0,1], [1, -1]. Aký je najmenší možný polomer kruhu na ktorom ležia?
Výsledok by mal byť 1,25.
Vedeli by ste mi prosím poradiť postup riešenia?
Ďakujem.
Dobrý deň,
ďakujem za odpoveď.
Body nemusia ležať na kružnici (hranici kruhu) ale aj v kruhu. M, teda počet bodov ktoré v kruhu ležia môže byť menší ako N, teda celkový počet bodov. 3 body bol len príklad, ich počet môže byť z uzavretého intervalu 1 až 400.
Domnievam sa, žiaľ neviem to dokázať, že ak má byť polomer čo najmenší tak (prevdepodobne, no vôbec si niesom istý) bude aspoň jeden z N bodov ležať na kružnici s rovnakým polomerom ako kruh. Ak bude počet bodov M menší, tak by som odobral z našej množiny bodov bod, ktorý na kružnici leží a postup opakoval až kým by v kruhu (alebo na jeho hranici) neležalo M bodov.
Mohol by som poprosiť všeobecnejšie riešenie?
0x
Tři body ze tří, to je ten snad nejjednoduččí případ, a v něm se skutečně jedná o kružnici opsanou. Obecný případ /počínaje třemi bony z více než tří, mi uý tak jednoduchý nepřijde, musím se hodně zamyslet; jaký je původ tohoto příkladu? A můýete upřesnit, zda v tom kruhu má ležet nejméně M bodů, nebo přesně M?
Platí 1<=M<=N<=400. Toto je originálne zadanie:
"You are given N points on 2-D plane. You have to find out minimal radius of a circle which contains at least M of these points."
Takže musí byť NAJMENEJ M bodov.
Keďže je to programátoská úloha vyžaduje sa, samozrejme, výhradne všeobecné riešenie.
Děkuji za upřwsnění. Ono, když jsem si to rozmyslel, by to ani jinak nemělo dobrý smysl, kdumyste měl všechny body na jedné kružnici, tak byste žádně odebrat nemohl.
Jinak k vaší první poznámce výše" máte pravdu, že aspoň jjeden bid musí být na kružnici, Kdyby tomu tak nebylo, našel bych mezi těmi vnitřními body ten, který je naší kružnici nejblíže a sestrojil bych soustřednou kružnici, jdoucí tímto bodem.
:Co víc, když už dostanu jeden bod na kružnici a ostatní budou stále uvnitřm vezmu ten jeden jako střed stejnolehlosti a vhodou stejnolehlostí tu kružnici zmenším tak, aby procházela ještě dalčímbodem. A to už nebudu rozvádět, ale nemělo by být těžké tu kruýnici, při zachování incidence s jeá vyznačenými dvěma body, zmenčit a dostat na ni třetí bod. Takře závěr by byl, že hledaná kružnice musí procházet alespoň třemi body (samozřejmě pokud v samotnám zadání není těch bodů méně. A z toho by mohlo vycházet řešení. Nebylo by moc "chytré" pro "ruční " řešení, ale programátorskému zadání by to odpovídalo. Prostě bych vyznačil všechny možné trojice a sestrojil kružnice jim opsané. Následně bych je pak probíral od nejmenšího poloměru a počítal, kolik bodu je uvnitř. Až by jich bylo M, byla by uloha řešena, Bylo by to sice práco jako na kostele, ale odt toho počítače jsou, ne?
Ďakujem veľmi pekne,
ano, už z časového limitu úlohy je vidieť, že bude veľmi zložitá a plná operácií, limit sú 2 sekundy - to je veľmi veľa.
Aj tak uvažujem, či sa to nedá urobiť ešte o trošku efektívnejšie - uvažoval som, že by sme robili trojuholníky len z bodov konvexného obalu (to by asi nebolo korektné).
Totiž, budem musieť urobiť všetky kombinácie a pri každej jednej kombinácii otestovať všetky najviac body.
Korektné riešenie už jednoznačne máme, otázka je či sa nedá časovo zjednodušiť.
Ešte raz veľmi pekne ďakujem.
Problém je ovšem v tom, že jsem se trochu ukvapil,. Ono to, že ta kružnice musí obsahovat alespon dva body je pravda, ale s těmi třemi bidy to tak jednoduché není. Třeba když mám tři body, leřící na usečce, nebo aby to nebylo tak extrémní, tak trodmě "placatý" trojúhelník, pak minimílní kružnice nebude těm třem bodům opsaná, ale taková, že dva body budou koncové body jejího průměru a třetí bude někde uvnitř. A jsem nahraný, nevím, co s tím. Omlouvám se..
Rozumiem. A je pravidlo, že 2 body musia ležať na kružnici? Čo ak by sme robili kružnicu zo všetkých možností dvoch bodov. Vtedy by asi nemusel by každý bod v kruhu.
Něco takového mne teky napadlo. Doufám, že v tom tvrzení, že u minimállní kruřnice musí být arpoň dva body na ní, je pravdivé, ale problém je v tom, že na rozdíl od tří bodů dva body kružnici neurčijé . Samozřejmě určují takovou tu nejmenčí, pro kterou dělají průměr, ale jak říkáte, ta nemusí ohraničovat dost bodů.
Možná by to šlo nějak zvládnout nějakým trikem, zatím nevím jakým, ale spíš bych hledal jinou cestu. Asi to řešení, až ho najdeme, bude jednoduché, ale zatím mne nenapadá.
Vpodstatě bych potřeboval pro obecný bod roviny a pro N vybraných bodů (ten vvýběr bych musel střídat ) najít maxumum jeho vzdálenosti od těch bodů N-tice (jinými slovy, mezi N ody najít ten nejvzdálenější) a nýsledně pak najít minimum takto vzniklé funkce přes všechny body roviny. A to udělat pro všechny N-tice a z výsledků najít ten nejmenší. Zkste uvažovat tímto směrem. Nevím, jak je to schůdné, ale když zjistíte oblast, pro kterou je ten který bod N.tice nejvzdálenější, tak byste pak v této oblasti mmusel najít nejbližší bod k tomu zkoumanému, což by byl stčd té hledané kružnice.
Ale mořný by ta cesta přes všechby dvojice byla schudnejší, i když nevím, jak by vypadala. Prostě vzít dva body , jimi vést kružnici a měnit její poloměr, dokud by nespolkla dost bodů.
Ak tomu správne rozumiem, tak by ste vzali všetky možné N-tice bodov, pričom, ich počet by bol taký, aké je naše minimum bodov, ktoré musia byť v kruhu. Otázka znie ako zostrojiť takúto kružicu, resp. kruh v ktorom sú dané body. A chcel som sa ešte opýtať: Nedá sa zostrojiť kružnica opísaná konvexnému obalu, resp. konvexnému mnohouholníku.
Žiaľ ta možnosť cez všetky dvojice nie je možná, naše body sú z množiny reálnych čísel a tak nie je možné rozpínať kružnicu, ak by boli celé čísla by sme to po jednom centimetry mohli zvyšovať.
Jde taky o to jestli se jedna o body, ktere vytvoří nějaky obrazec, který potom vytvoři kružnici opsanou. Nebo jestli jde o body, které vytvoří oblouk. V tom prvním připadě to je lehke, v tom druhem to bude oříšek, protože neznaš vyšku ani poloměr oblouku (ale určitě to nějak jde, autocad to umi).
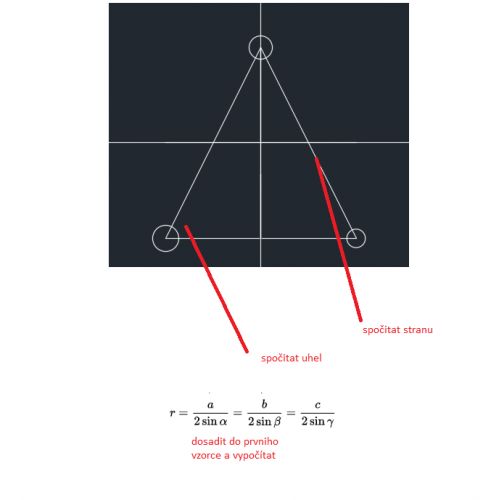
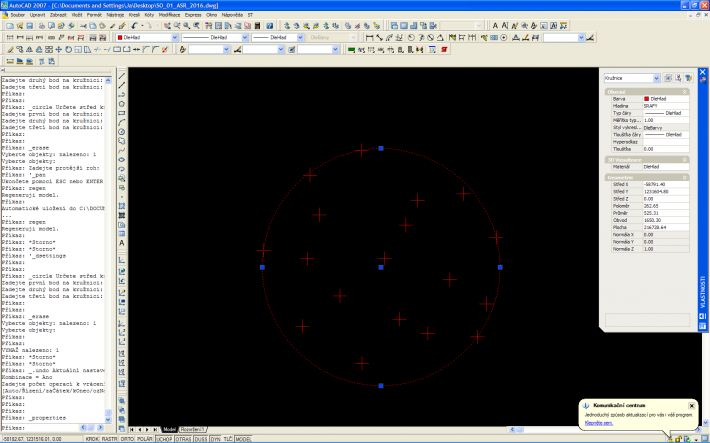
Skúsil som si to urobiť v Autocade, tam som našiel možnosť vytvoriť pomocou 3 bodov kružnicu tak som si vzal body, ktoré sa mi "zdali", že by to mohli byť právne tie. Potom už len stačí použiť vzorec pre opísanú kručnicu a je to. Ako to urobiť číselne, lebo v autocade som to spravil len "od oka", teda ako sa dá nájsť dané body?
Nenesieme zodpovednosť za správnosť informácií a za škodu vzniknutú ich využitím. Jednotlivé odpovede vyjadrujú názory ich autorov a nemusia sa zhodovať s názorom prevádzkovateľa poradne Poradte.sk
Používaním poradne súhlasíte s personalizovanou reklamou, ktorá pomáha financovať tento server, ďakujeme.